Number Theory has a long history in Asia, and Asians have made and will certainly continue to make many outstanding contributions to the field. The aim of the annual Pan Asian Number Theory (PANT) Conferences is to encourage research in number theory in present-day Asia and foster collaborations among young number theorists in Asia and beyond. Since 2009, PANT conferences have been held in Korea, Japan, China, India, Vietnam, and Singapore. The eleventh PANT Conference (PANT 2023-Harbin) will be held at IASM, Harbin Institute of Technology in Harbin from August 1 - 5, 2023. The conference will consist of about 25 one-hour invited lectures. Everyone is welcome!
Scientific Committee:
YoungJu Choie (Pohang)
Wee Teck Gan (NUS)
Tamotsu Ikeda (Kyoto)
Kazuya Kato (Chicago)
Minhyong Kim (Edinburgh)
Masato Kurihara (Keio)
Wen-Ching Winnie Li (Penn State)
Jianya Liu (Shandong)
Bao Chau Ngo (Chicago)
Dipendra Prasad (IIT)
Sujatha Ramdorai (British Columbia)
Ye Tian (AMSS, CAS)
Organizing Committee:
Wee Teck Gan (NUS)
Chunhui Liu (Harbin)
Bao Chau Ngo (Chicago)
Quanhua Xu (Harbin)
Yichao Zhang (Harbin)
Abstract: In the 1970s, nearly holomorphic modular forms and the non-holomorphic operators, the Maass-Shimura operators, were studied extensively by Shimura. Later on, he discovered their connection with the periods of CM elliptic curves.
In this talk, we introduce the notion of nearly holomorphic Drinfeld modular forms and construct an analogue of the Maass-Shimura operators in this context. Furthermore, we investigate the relation between the periods of CM Drinfeld modules and the special values of nearly holomorphic Drinfeld modular forms at CM points. This is joint work with Oguz Gezmis.
Abstract: I will talk about the twisted moments of central L-values for GL(2) Maass forms over imaginary quadratic fields. As a direct consequence, it can be shown that at least 33% of such central L-values do not vanish. This is joint work with Sheng-Chi.
Abstract: Progress on some classical questions in analytic number theory has been
relied, via character sums of various shape, on Deligne's proof of the Riemann Hypothesis over finite fields. In this talk we will discuss several applications of trace functions of 
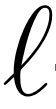-adic sheaves in this regard and how trace functions interact with Fourier coefficients of automorphic forms.
